Da li je 50 godina star matematički problem mogao da spase Luvr od pljačke

Posle smele krađe u Luvru, lopovi su usred bela dana uspeli da pobegnu sa neprocenjivim krunskim nakitom - evo kako decenijama star geometrijski problem može da pomogne muzejima da unaprede obezbeđenje.

Trebalo im je svega osam minuta.

Za tih 480 sekundi, lopovi su se popeli uz mehaničku platformu da bi stigli do balkona na prvom spratu muzeja Luvr u Parizu, da bi potom upali kroz izrezani prozor usred bela dana.

Kad su ušli, provalili su dve staklene vitrine, a potom pobegli sa osam primeraka neprocenjivog krunskog nakita tiz vremena Napoleona.

Bila je to „smela krađa" koja je potresla Francusku do srži.

Do sada je uhapšeno sedmoro osumnjičenih u vezi sa ovom krađom.

OVDE pogledajte grafički prikaz velike pljačke Luvra koja je zaprepastila Francusku.

Jedno od čestih pitanja bez odgovora koje muči istražitelje bilo je zašto lopovi nisu bili otkriveni ranije.

Na saslušanju pred Francuskim senatom neposredno posle pljačke, Lorans de Kars, direktorka svetski slavnog muzeja, priznala je da „nisu uspeli da zaštite" krunski nakit.

Jedina kamera koja je pokrivala balkon na koji su lopovi ušli, nastavila je, bila je uperena u pogrešnom pravcu, a preliminarni izveštaj je otkrio da svaka treća prostorija u krilu Denon na koju su lopovi udarili nije imala sigurnosne kamere.

Generalnije gledano, De Kars je priznala da su smanjenja broja pripadnika obezbeđenja učinila muzej ranjivijim i insistirala na tome da sigurnosni sistem Luvra mora da se pojača tako da može da se „motri" svaka tačka.

Alarmi u muzeju su se navodno oglasili kad je trebalo, prema francuskom Ministarstvu za kulturu.

Pogledajte kako su lopovi pobegli iz Luvra posle pljačke

Opet, ovo je treća krađa u francuskim muzejima za dva meseca, što je nateralo Ministarstvo da sprovede nove planove obezbeđenja širom Francuske.

Iako nema nikakve sumnje da je savremeno obezbeđivanje muzeja složena i skupa rabota, postoji intrigantan 50-godišnji matematički problem koji se bavi upravo ovim problemom.

On se pita koji je minimalni broj čuvara - ili, ekvivalentno, sigurnosnih kamera sa rasponom od 360 stepeni - neophodan da bi se čitav muzej držao pod prismotrom?

Ovo je poznato kao problem muzeja, ili problem likovne galerije.

Rešenje je veoma elegantno.

Pretpostavićemo da su svi zidovi našeg imaginarnog muzeja pravih linija tako da je tlocrt ono što matematičari zovu poligonom, oblik sa oštrim ivicama i uglovima.

Kamere moraju da budu na fiksnim položajima, ali mogu da vide u svim pravcima.

Da bismo bili sigurni da je pokriven čitav muzej, morali bismo da možemo da povučemo pravu liniju iz bilo koje tačke na tlocrtu do najmanje jedne od kamera.

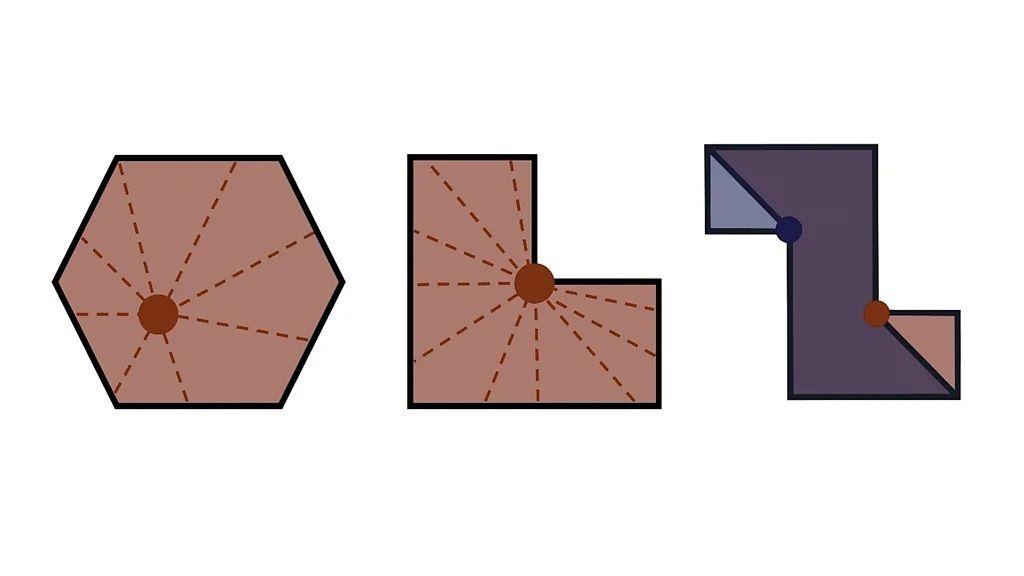
Uzmite na primer galeriju heksagonalnog oblika levo na dijagramu ispod.

Bez obzira na to gde postavite kameru, moći ćete da vidite čitav sprat i zidove čitavog prostora.

Kad na ovaj način svaki položaj može da se vidi iz svakog drugog, mi oblik galerije nazivamo konveksnim poligonom.

Galerija u obliku slova L u sredini je nekonveksna, što znači da ste ograničeni u vašem postavljanju kamera, ali i dalje možemo da pronađemo tačke iz kojih jedna kamera može da vidi čitavu galeriju.

Galeriji oblika A-Z potrebne su dve kamere da bi je pokrili - uvek postoje tačke koje će samo jedna kamera promašiti.

Za interesantnije tlocrte (pogledajte neobičan 15-stranični tlocrt ispod) mnogo je teže znati koliko kamera je potrebno ili gde one treba da stoje.

Srećom po direktore muzeja ograničenih muzeja, češki teoretičar grafova Vaclav Hvatal rešio je opšti problem muzeja nakon što je ovaj bio postavljen 1973. godine.

Odgovor, ispostavilo se, zavisi od broja uglova (ili, kako ih matematičari zovu, „temena"), jer će biti onoliko zidova koliko je uglova u prostoriji.

Malo prostog deljenja pomaže nam da izračunamo koliko je kamera potrebno.

Deljenjem broja uglova u prostoriji sa brojem tri, saznaćemo koliko kamera je potrebno da ona bude potpuno pokrivena, pod pretpostavkom da kamere imaju preglednost od punih 360 stepeni.

Ovo funkcioniše čak i za složene oblike kao što je neobična 15-strana galerija na slici ispod.

U ovom slučaju ima 15 uglova, dakle 15 podeljeno sa tri je pet.

Ovo funkcioniše čak i ako broj uglova nije deljiv sa tri.

Za galeriju sa 20 strana, na primer, rešenje je šest i dve trećine.

U ovim slučajevima možete da uzmete samo ceo broj - dakle, ne bi nam bilo potrebno više od šest kamera u prostoriji sa 20 strana.

Stiv Fisk, profesor matematike na koledžu Boudon u Mejnu, u SAD, 1978. godine je pronašao dokaz, koji se smatra jednim od najelegantnijih u čitavoj matematici, za ovu nižu granicu broja neophodnih kamera.

Njegova strategija bila je da podeli galeriju u trouglove (pogledajte levu sliku figure ispod).

On je potom dokazao da možete da izaberete samo tri boje - na primer, crvenu, žutu i plavu - i dodelite različitu boju uglovima svakog trougla.

To bi značilo da svaki trougao u vašoj galeriji ima različitu boju u vlastita tri ugla (pogledajte desnu sliku figure ispod, za primer).

To je poznato kao „trobojenje" uglova.

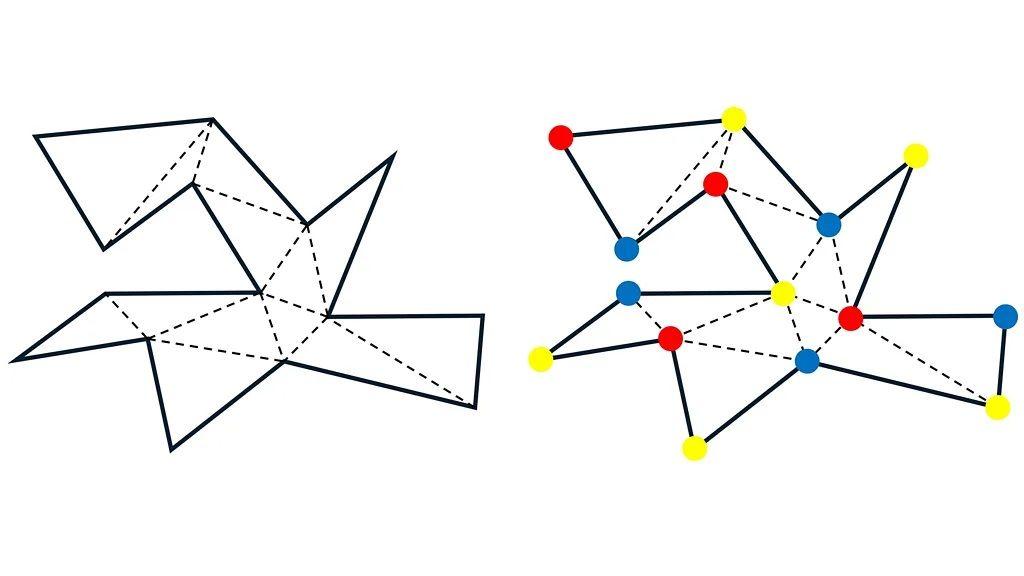
Trouglovi su jedni od onih „konveksnih" poligona koje smo pominjali ranije, tako da kamera postavljena u bilo koji ugao (ili zapravo bilo gde u trouglu) može da vidi svaku tačku u tom obliku.

Svaki trougao ima uglove sa svakom od tri boje.

To znači da možete da odaberete samo jednu od boja i stavite kameru na te položaje.

Te kamere će moći da vide svaki deo svakog trougla i stoga svaki deo galerije.

Ali evo najboljeg dela.

Lepota Fiskovog dokaza krije se u tome da možete da odaberete boju sa najmanje tačaka, a i dalje ćete pokriti čitavu galeriju.

Na obliku sa 15 strana iznad, biranjem crvenih tačaka možemo da se izvučemo sa samo četiri kamere.

Štaviše, crvena tačka u gornjem levom uglu nije neophodna, zato što sledeća crvena kamera može da pokrije čitav njen prostor za nadzor.

Dakle, mogli bismo čak da se izvučemo sa tri kamera za ovu galeriju.

• Kuća mudrosti - mesto nastanka savremene matematike
• Jesu li neki ljudi prirodno loši u matematici
• I životinje razumeju brojeve - to im pomaže da prežive

Ovo je posebno tačno ako instaliramo moderne kamere sa više pravaca, umesto širokougaone sigurnosne kamere stare škole koje bi morale stalno da prebrišu prostor da biste dobili potpuni pregled, privremeno stvarajući mrtve uglove.

Ali ne treba zaboraviti da mnogi tradicionalni muzeji kao što je Luvr imaju uglavnom pravougaone prostorije.

Srećom, varijacija na problem likovne galerije pokazuje da kad se zidovi spajaju pod odgovarajućim uglovima, potrebna nam je samo jedna kamera da pokrijemo čitavu prostoriju.

U svedočenju, De Kars je priznala i da spoljne kamere Luvra ne pokrivaju sve zidove.

„Nismo primetili dolazak lopova dovoljno rano... slabost zaštite našeg perimetra dobro je poznata", rekla je ona.

Srećom, postoje verzije ovog problema, poznate kao „problem tvrđave" ili „problem zatvora", koje rešavaju problem pokrivenosti kamerama i za spoljašnjosti neke građevine.

Zvaničnici Luvra priznaju da bezbednosne kamere nisu pokrivale čitavu spoljašnjost zgrade

Ono što, međutim, otkrivaju obe varijante je da je pronalaženje prave tačke posmatranja od ključne važnosti.

Ali samo je važno prihvatiti da lopovi koji ulaze kroz javne galerije nisu jedina pretnja sa kojom se suočavaju muzeji.

Britanskom muzeju u Londonu, na primer, dogodilo se da Kartijeov prsten vredan 950.000 dolara nestane 2011. godine iz kolekcije koja nije bila javno izložena.

Dragulji iz muzeja bili su pronađeni u oglasu na iBeju 2020. godine nakon što ih je navodno uzeo jedan od kustosa muzeja.

Pored krađe, muzeji takođe moraju da zaštite kolekcije od vandalizma, požara i drugih oblika uništavanja.

Uprkos tome, problem likovne galerije je vredan pažnje čak i onima izvan svetih muzejskih prostora.

On ima primenu na širokom dijapazonu polja gde su vidljivost i pokrivenost od ključne važnosti.

U robotici, na primer, on pomaže autonomnim sistemima da poboljšaju efikasnost i spreče sudaranja.

U urbanom planiranju, on utiče na pozicioniranje radio antena, tornjeva za prenos signala mobilne telefonije ili detektora zagađenja kako bi osigurali sveobuhvatnu pokrivenost javnih prostora.

Strategije upravljanja katastrofama koriste slične principe za postavljanje dronova za nadzor lokacija katastrofa širokih razmera iz vazduha ili da bi postavili poljske medicinske stanice.

U montaži pokretnih i kompjuterskih slika, problem likovne galerije može da pomogne u identifikovanju vidljivih regija u okviru neke scene.

On može da pomogne da osigura da su glumci uvek osvetljeni na sceni i čak pomogne samim muzejima da osiguraju da su njihove galerije odgovarajuće osvetljene.

Luvr nije odgovorio na pitanja BBC-ja da li je bio svestan rešenja koje nudi matematički problem muzeja.

Muzej, nesumnjivo, trenutno ima veće probleme koje mora da reši.

Ali dok muzeji i likovne galerije širom sveta preispituju vlastitu sigurnost posle krađe u Luvru, ne može da škodi podsetiti se lekcija koje nudi ovaj 50 godina star matematički problem.

Pogledajte video: Neki od dragulja ukradenih iz Luvra

BBC na srpskom je od sada i na Jutjubu, pratite nas OVDE.

Pratite nas na Fejsbuku, Tviteru, Instagramu, Jutjubu i Vajberu. Ako imate predlog teme za nas, javite se na bbcnasrpskom@bbc.co.uk

• Luvr opljačkan za sedam minuta: 'Zakazali smo', priznala direktorka muzeja
• Pljačka u Luvru: Nova hapšenja, neki osumnjičeni 'delimično priznali' krivicu
• Vrednost ukradenih dragulja iz Luvra procenjena na 88 miliona evra: tužiteljka
• Ukradeni dragulji u Luvru, kruna ispuštena tokom bekstva i ozbiljna pitanja o bezbednosti
• Četiri velike pljačke muzeja u Srbiji
• Koliko je lako ukrasti predmete iz muzeja

(BBC News, 10.31.2025)